Dziwne liczby Lucasa to ciąg liczb stworzony przez francuskiego matematyka. Wiele osób określa je mianem niezwykłych, fenomenalnych lub wręcz rewolucyjnych. Ich zdefiniowanie nastąpiło u schyłku XIX wieku, za ich podstawowe zadanie uważa się możliwość wyszukiwania liczb pierwszych. Jednak ciągi liczbowe Lucasa znajdują również zastosowanie w algorytmach szyfrowania.

Kim był Lucas?

François Édouard Anatole Lucas był francuskim matematykiem, który przyszedł na świat w 1842 roku, zaś zmarł w 1891.

Skończył studia w Ecole Normale Superieure w Paryżu, służył również w szeregach armii francuskiej, pracował jako profesor matematyki w Paryżu.

Jego praca naukowa koncentrowała się wokół algebry.

Stworzony przez niego ciąg liczbowy został nazwany od jego nazwiska ciągiem Lucasa.

Poświęcił sporo czasu na badanie doskonale znanego ciągu Fibonacciego i stworzył wzór, pozwalający na określenie n-tego wyrazu tegoż ciągu.

Pośród jego dokonań wymienia się również opracowanie testu pozwalającego na badanie pierwszości liczb, tzw. test Lucasa-Lehmera.

Pośród jego licznych zainteresować znajdowało się również rozrywkowe wykorzystanie zagadnień matematycznych.

W 1883 roku wymyślił i stworzył grę o nazwie Wieże Hanoi, jednak jej sprzedaż prowadził pod pseudonimem.

Mimo wszystko jednak w historii najsilniej zapisał się on jako twórca ciągu Lucasa.

Jest on może nieco rzadziej przytaczany niżeli słynne dzieło Fibonacciego, jednak od strony matematycznej zdecydowanie bliżej mu do złotej proporcji.

Złota zasada

Została po raz pierwszy ukazana w znanym dziele Fibonacciego.

Jego ciąg liczbowy rozpoczyna się od jedynek i powstaje na skutek dodawania dwóch kolejnych cyfr do siebie.

Jednocześnie dzielenie kolejnych elementów przez siebie pozwala nam na uzyskanie tzw. złotej liczby.

W pierwszym momencie można stwierdzić, że taka właściwość będzie całkowicie unikalna w ciągu liczbowym, i stąd wielka sława tychże liczb.

Jednak niekoniecznie.

Udowodniono, że można wybrać dwie dowolne liczby i na ich bazie dokonać zbudowania ciągu liczbowego, kierując się identyczną zasadą jak w ciągu Fibonacciego, a również w nim uzyskamy możliwość odnalezienia złotych podziałów.

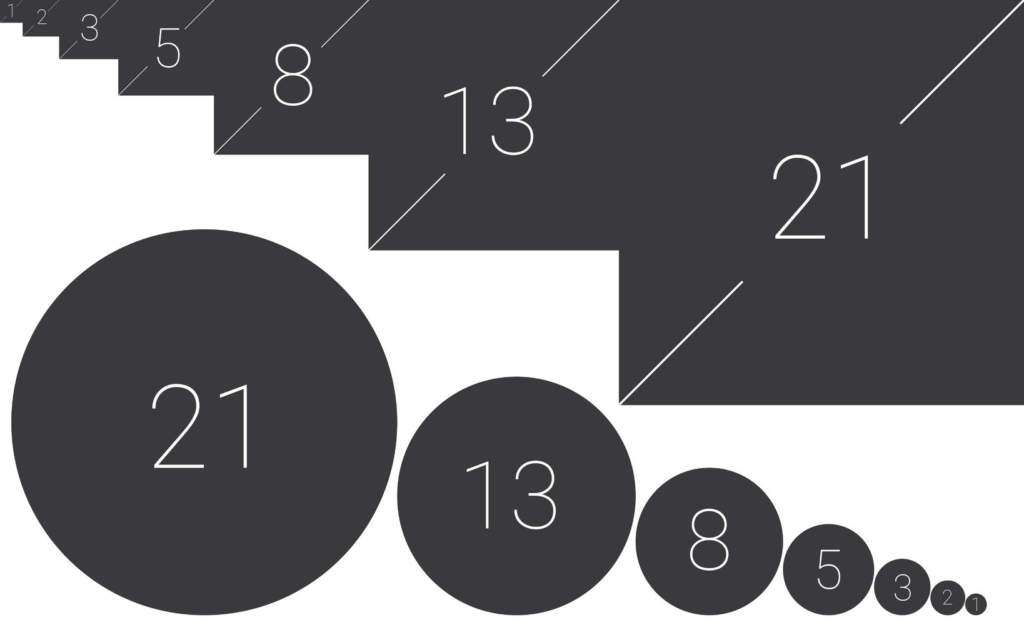
Można więc mówić o całej grupie złotych ciągów.

I podstawowym wyznacznikiem nie będą tu liczby, od których rozpoczniemy, ale metoda powstawania ciągu nazywana złotą zasadą.

Ciąg Lukasa określa się wedle następujących określeń rekurencyjnych:

L₀= 2

L₁=1

L_n=L_n-1+L_n-2 , dla n>1

Ciąg Lukasa, w początkowych wartościach, prezentuje się następująco:

2, 1, 3, 4, 7, 11, 18, 29, 47, 76, 123, 199, 322, 521, 843, 1364, …

Przy założeniu, że F_n to n-ta liczba ciągu Fibonacciego, ciąg Lucasa prezentuje następujące równości:

L_n= F_n-1+ F_n+1

5F_n= L_n-1 +L_n+1

F_2n= L_nF_n

Jak widać wyżej, powstawanie ciągu Lucasa opiera się o złotą zasadę.

Tak jak u Fibonacciego stosunek każdego kolejnego elementu do poprzedniego będzie zbiegał do Φ.

Jest to jednak podstawowa zasada każdego złotego ciągu, pytanie więc brzmi, co takiego wyjątkowego ma w sobie ciąg liczbowy Lucasa?

Po dokładnym przeanalizowaniu zapisu stworzonego przez Lucasa okazuje się, że następne liczby jego ciągu stanowią zaokrąglenia kolejnych potęg liczby Φ.

Przedstawia się to następująco:

Φ⁰ = 1

Φ¹ = 1,618033988 czyli w przybliżeniu 2

Φ²= 2,618033988 czyli w przybliżeniu 3

Φ³ = 4,236067977 czyli w przybliżeniu 4

Φ⁴= 6,854101954 czyli w przybliżeniu 7

Φ⁵= 11,09016942 czyli w przybliżeniu 11

Φ⁶ = 17,94427190 czyli w przybliżeniu 18

Φ⁷ = 29,03444184 czyli w przybliżeniu 29

Φ⁸= 46,97871375 czyli w przybliżeniu 47

Można kontynuować to w nieskończoność i zawsze kolejne liczby ciągu Lucasa będą stanowiły potęgę liczby Φ.

Te wspaniałe zależności wykorzystuje się powszechnie w tworzeniu algorytmów do szyfrowania.

Jednak pomimo tak spektakularnego i ponadczasowego zapisu, jego twórca nie został silnie zapamiętany, a jego nazwisko znane jest jedynie wybranym.

Być może dlatego, że matematyka nie jest dziedziną dla każdego.

WSPARCIE NIEZALEŻNYCH PORTALI

*Niebieską czcionką zaznaczono odnośniki np. do badań, tekstów źródłowych lub artykułów powiązanych tematycznie.