Hipoteza Poincarégo była jednym z problemów milenijnych, ogłoszonych przez Instytut Matematyczny Claya w 2000 roku. Jak wiadomo, istnieją bowiem problemy naukowe, nad którymi badacze głowią się długimi miesiącami lub nawet latami. Kolejne pokolenia poszukują odpowiedzi. Do takich właśnie zagadnień zaliczała się od 1904 roku hipoteza postawiona przez francuskiego matematyka i fizyka Julesa Heinriego Poincarégo. Badacz zamknął w lakonicznej formie niezmiernie istotną hipotezę, która opisuje właściwości kształtu przestrzeni.

Sedno hipotezy

Sama hipoteza postawiona przez naukowca ponad 100 lat temu brzmi:

Każda trójwymiarowa zwarta i jednospójna rozmaitość topologiczna bez brzegu jest homeomorficzna ze sferą trójwymiarową, czyli brzegiem czterowymiarowej kuli.

Oprócz ogólnych rozważań matematycznych, w znacznym uproszczeniu, francuski badacz skupił się na analizie natury przestrzeni trójwymiarowych, a sama hipoteza stała się kluczem do rozwoju nauki zwanej topologią, która zajmuje się badaniem właściwości figur geometrycznych, w szczególności ich przekształceń.

Do głównych jej zadań należy opisywanie i klasyfikowanie zbiorów z pomocą homeomorfizmów, czyli takiego wyginania powierzchni figur czy brył, aby jej nie przerwać.

Z tą dziedziną wiążą się też wymienione w definicji rozmaitości topologiczne, czyli grupy obiektów geometrycznych, zajmujących konkretną przestrzeń.

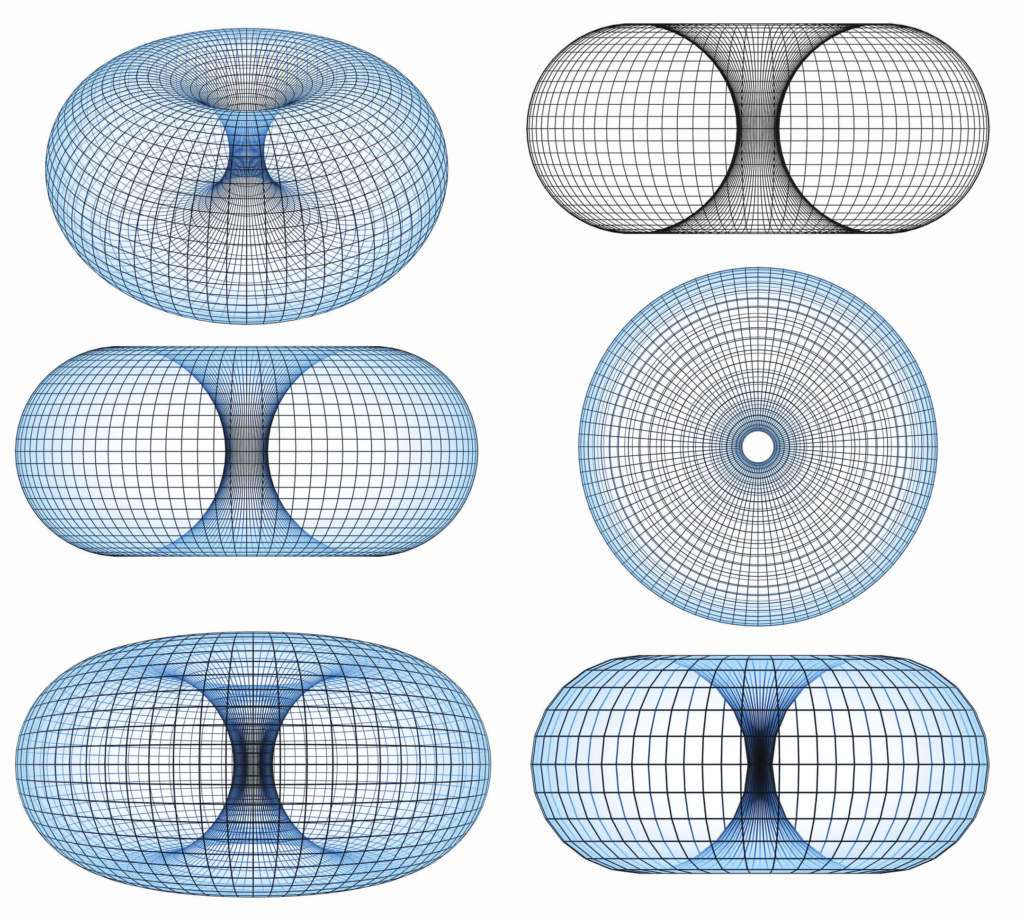
W przypadku rozmaitości dwójwymiarowych, do obiektów zwartych, które mają dwie strony, ale nie mają brzegów ani żadnych nakłuć czy rozcięcia, zalicza się: sferę, torusa i precla.

Są to obrotowe powierzchnie dwuwymiarowe, które zanurzono w przestrzeni trójwymiarowej.

Kształt przestrzeni

Kiedy mówimy o powierzchni zwartej i jednospójnej rozmaitości topologicznej, jest to forma najprostsza.

W przypadku rozmaitości jednowymiarowych nie ma takiej struktury, w przypadku dwuwymiarowych jest jedna – sfera.

W ramach analizowanych przez Poincarégo rozmaitości trójwymiarowych, według badacza, jest również tylko jeden przykład – sfera trójwymiarowa.

Rozmaitości są zwarte, gdy są ograniczone i domknięte.

Z kolei jednospójność pojawia się, gdy niezależnie od położenia możemy bez przeszkód zmniejszać pętlę, bez wychodzenia poza powierzchnię rozmaitości, aż do uzyskania punktu.

Obrazowo wyjaśniając – hipoteza Poincarégo związana jest z poszukiwaniem sposobu na przekształcenie dętki w sferę tylko za pomocą rozciągania i wyginania, unikając przecięć.

Potwierdzenie hipotezy Poincarégo – strapienie pokoleń matematyków

Przez wiele lat nad potwierdzeniem tez Francuza głowili się najwybitniejsi matematycy.

Od lat 50. i 60. XX wieku tym problemem zajmowali się: Wolfgang Haken i Kristos Papakiriakopulos (nazywany Papą).

Niestety nigdy nie udało im się znaleźć w pełni prawdziwego dowodu, choć spędzili na jego poszukiwaniach większą część życia, wpadając w obłęd lub tracąc przy tym zdrowie.

Później swych sił próbowali również Stephen Smale oraz Willam Thurston, który sformułował znacznie ogólniejsze założenia.

W roku 2000 hipoteza, jako istotny, ale wciąż nierozwiązany problem znalazła się na opublikowanej przez Instytut Matematyczny Claya liście siedmiu problemów milenijnych, czyli najważniejszych zagadnień matematycznych, które stawały się wyzwaniem dla matematyków nowego tysiąclecia.

I to właśnie hipoteza Poincarégo jako pierwsza doczekała się rozwiązania.

Dokonał tego rosyjski uczony Grigorij Perelman, jeden z najinteligentniejszych umysłów współczesnego świata, który hipotezą zainteresował się już w latach 90. XX wieku, a jej potwierdzenie ogłosił w 2002 roku.

W swym dowodzie korzystał z wcześniejszych dokonań innych matematyków m. in. Hamiltona oraz wspomnianego wcześniej Thurstona.

Przeanalizowanie jego dowodu trwało niemal cztery lata.

Jednak w 2006 roku finalnie potwierdzono słuszność jego dowodzeń, tym samym uznając, że jako pierwszemu udało mu się rozwiązać jeden z problemów milenijnych.

Jego dokonanie miało tak wielkie znaczenie, że ogłoszono je matematycznym odkryciem roku 2006 przez magazyn Science.

Co ciekawe, rosyjski matematyk twierdził, że nie dokonał niczego wielkiego i nie potrzebuje rozgłosu.

W dniu 23 sierpnia 2006 roku, gdy miał odebrać w Madrycie prestiżowy medal Fieldsa (odznaczenie, nazywane matematycznym Noblem), nie stawił się na rozdaniu nagród, a potem odmówił przyjęcia nagrody w wysokości miliona dolarów, przyznanej mu przez amerykański Instytut Matematyczny Claya z Cambridge w stanie Massachusetts.

WSPARCIE NIEZALEŻNYCH PORTALI

*Niebieską czcionką zaznaczono odnośniki np. do badań, tekstów źródłowych lub artykułów powiązanych tematycznie.